Question

The number of weaving errors in a twenty-foot by ten-foot roll of carpet has a mean of 0.8 What is the probability of observing more than 4 errors in the carpet

Answer 1

0.14% probability of observing more than 4 errors in the carpet

Step-by-step explanation:

When we only have the mean, we use the Poisson distribution.

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

The number of weaving errors in a twenty-foot by ten-foot roll of carpet has a mean of 0.8.

This means that
`\mu = 0.8`

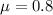
What is the probability of observing more than 4 errors in the carpet

Either we observe 4 or less errors, or we observe more than 4. The sum of the probabilities of these outcomes is 1. So

`P(X \leq 4) + P(X > 4) = 1`

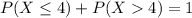
We want P(X > 4). Then

`P(X > 4) = 1 - P(X \leq 4)`

In which

`P(X \leq 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-0.8)*(0.8)^(0))/((0)!) = 0.4493`

`P(X = 1) = (e^(-0.8)*(0.8)^(1))/((1)!) = 0.3595`

`P(X = 2) = (e^(-0.8)*(0.8)^(2))/((2)!) = 0.1438`

`P(X = 3) = (e^(-0.8)*(0.8)^(3))/((3)!) = 0.0383`

`P(X = 4) = (e^(-0.8)*(0.8)^(4))/((4)!) = 0.0077`

`P(X \leq 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0.4493 + 0.3595 + 0.1438 + 0.0383 + 0.0077 = 0.9986`

`P(X > 4) = 1 - P(X \leq 4) = 1 - 0.9986 = 0.0014`

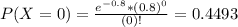
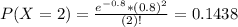
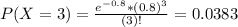
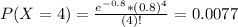
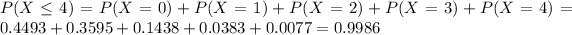
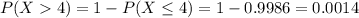
0.14% probability of observing more than 4 errors in the carpet