Question

One canned juice drink is 25% orange juice another is 10% orangw juice. How many liters of each should be mixed together in order to get 15 Lbthat is 20% orange juice?

Answer 1

There should be 10 l of 25% orange juice and 5 l of 10% orange juice.

Explanation:

Let the amount of the 25% orange juice be "x", while the amount of the 10% one be "y". The sum of these must be equal to 15 l, therefore:

`x + y = 15`

The sum of the concentration of juice on each can must be equal to the final product, therefore:

`25\%*x + 10\%*y = 15*20\%\\0.25*x + 0.1*y = 3`

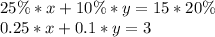
We can now solve the system of equations as shown below:

`\left \{ ({{x + y=15})*(-0.1) \atop {0.25*x + 0.1*y=3}} \right. \\\left \{ {{-0.1*x - 0.1*y=-1.5} \atop {0.25*x + 0.1*y=3}} \right. \\-0.1*x + 0.25*x = 3 - 1.5\\0.15*x = 1.5\\x = (1.5)/(0.15) = 10\\y = 15 - x = 15 - 10 = 5`

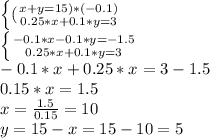
There should be 10 l of 25% orange juice and 5 l of 10% orange juice.