How many real solutions does this system of equations have? x2+y2=363x−y+1=0 A. 0 B. 3 C. 2 D. 1

Question

asked Jul 1, 2021 33.4k views

2 Answers

Brett Hall · Answer 1 · 2021-07-07T19:35:42+0000

Answer:

Correct option: C -> 2

Explanation:

The first equation is:

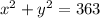
x^2+y^2=363

And the second equation is:

x-y+1=0

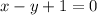
From the second equation, we have:

y = x + 1

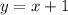
Using this value of y in the first equation, we have:

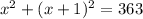
x^2 + (x+1)^2 = 363

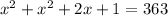
x^2 + x^2 + 2x + 1 = 363

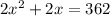
2x^2 + 2x= 362

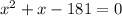
x^2 + x - 181 = 0

Calculating the discriminant Delta, we have:

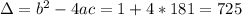
$\Delta = b^2 - 4ac = 1 + 4*181 = 725$

We have
$\Delta > 0$ , so we have two real values for x, therefore we have two solutions for this system.

Correct option: C.

(If the system of equation is actually:

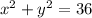
x^2+y^2=36

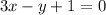
3x-y+1=0

We would have:

y = 3x + 1

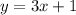
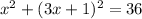
x^2+(3x+1)^2=36

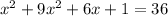
x^2+9x^2+6x+1=36

10x^2+6x-35=0

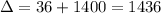
$\Delta = 36 + 1400 = 1436$

We also have
$\Delta > 0$ , so we have two solutions for this system.

Correct option: C.)