Answer:
appropriately writing the proportion can reduce or eliminate steps required to solve it
Explanation:
The proportion ...
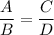
is equivalent to the equation obtained by "cross-multiplying:"
AD = BC
This equation can be written as proportions in 3 other ways:
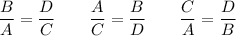
Effectively, the proportion can be written upside-down and sideways, as long as the corresponding parts are kept in the same order.
I find this most useful to ...
a) put the unknown quantity in the numerator
b) give that unknown quantity a denominator of 1, if possible.
__
The usual method recommended for solving proportions is to form the cross-product, as above, then divide by the coefficient of the variable. If the variable is already in the numerator, you can simply multiply the proportion by its denominator.
Example:
x/4 = 3/2
Usual method:
2x = 4·3
x = 12/2 = 6
Multiplying by the denominator:
x = 4(3/2) = 12/2 = 6 . . . . . . saves the "cross product" step
__
Example 2:
x/4 = 1/2 . . . . we note that "1" is "sideways" from x, so we can rewrite the proportion as ...
x/1 = 4/2 . . . . . . written with 1 in the denominator
x = 2 . . . . simplify
Of course, this is the same answer you would get by multiplying by the denominator, 4.
The point here is that if you have a choice when you write the initial proportion, you can make the choice to write it with x in the numerator and 1 in the denominator.