Question

Points P and Q belong to AB. If AB = a and AP = 2PQ = 2QB, find the distance between: the midpoints of AP and QB.

NO explanation needed. I need this fast

Answer 1

The distance between midpoint of AP and QB is
`(5a)/(8)`.

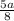Explanation:

Given that: AB = a

AP = 2PQ = 2QB

Thus,

PQ = QB =
`(a)/(4)`

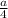
PQ + QB =
`(a)/(4)`+
`(a)/(4)`

=
`(a)/(2)`

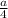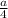
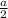
AP =
`(1)/(2)` a =
`(a)/(2)`

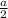
The distance between midpoint of AP and QB can be determined as;

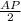`(AP)/(2)` + PQ +
`(QB)/(2)`

=
`(a)/(4)` +
`(a)/(4)` +
`(a)/(8)`

=
`(2a+2a+a)/(8)`

=
`(5a)/(8)`

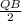
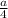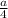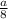
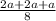
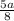
Therefore, the distance between midpoint of AP and QB is
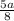`(5a)/(8)`.