Question

Suppose that we will randomly select a sample of 106 measurements from a population having a mean equal to 19 and a standard deviation equal to 7. Calculate the probability that we will obtain a sample mean greater than 21; that is, calculate P( x> 21).

Answer 1

The probability that we will obtain a sample mean greater than 21" is 0.00164 (
`\\ P(\overline{x}>21) = P(z>2.94) = 0.00164`).

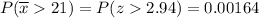Explanation:

The fundamental concept to understand to answer this question is, at least, the sampling distribution of means. Roughly speaking, this is the distribution of different means,
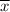`\\ \overline{x}`, of the random variable
`\\ x` for samples of the same size,
`\\ n`. That is, for each sample, we get its mean, and the probability distribution of them is called the sampling distribution of means.

As the sample size,
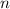`\\ n`, is greater, the distribution of
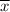`\\ \overline{x}` follows a normal distribution with mean that equals the population mean,
`\\ \mu`, and standard deviation that equals
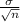`\\ (\sigma)/(√(n))`. This result is known as the Central Limit Theorem, and it is crucial in Statistical Inference. Mathematically:

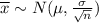`\\ \overline{x} \sim N(\mu, (\sigma)/(√(n)))` [1]

It is important to remember that this result is valid following the rule of thumb that the sample size,
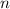`\\ n`, must be, at least, greater or equals to 30, that is,
`\\ n \geq 30`, no matter the distribution that follows
`\\ x` (this result is not important if

Another important concept is that the random variable
`\\ Z`, which is a standardized variable, that is, (roughly speaking) a variable that indicates the distance in standard deviations units from the mean,
`\\ \mu`, of a value in the distribution. In this case, the latter is
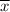`\\ \overline{x}`. We can express this mathematically as follows:

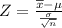`\\ Z = \frac{\overline{x} - \mu}{(\sigma)/(√(n))}` [2]

This variable
`\\ Z` follows a standard normal distribution or a normal distribution with
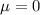`\\ \mu = 0` and standard deviation
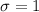`\\ \sigma = 1` or
`\\ Z \sim N(0, 1)`.

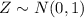With all this information, we can proceed to answer the question.

The probability that we will obtain a sample mean greater than 21

Or calculate
`\\ P(x>21)`.

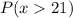For doing this, we have:

1. 
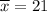   `\\ \overline{x} = 21`, which is the sample mean (a sample whose mean,
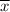   `\\ \overline{x}`, is 21.)
2. The sample size,
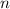   `\\ n`, is 106 or
   `\\ n = 106`.
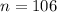3. The population's mean,
   `\\ \mu`, is 19 or
   `\\ \mu = 19`.
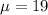4. The population's standard deviation,
   `\\ \sigma`, is 7 or
   `\\ \sigma = 7`.

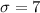Well, all we have to do is use [2] to calculate
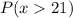`\\ P(x>21)` as follows:

`\\ Z = \frac{\overline{x} - \mu}{(\sigma)/(√(n))}`

`\\ Z = (21 - 19)/((7)/(√(106)))`

`\\ Z = (2)/((7)/(10.29563))`

`\\ Z = (2)/(0.67990)`

`\\ z = 2.94160 \approx 2.94`

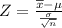
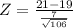
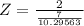
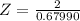
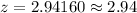
(We rounded this value to
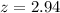`\\ z = 2.94` since standard normal tables have two digits for decimal part of
`z`. Notice we use z lowercase since z = 2.94 is a realization of random variable Z, and also that z is the standardized score for
`\\ \overline{x}`.)

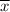With this value of z = 2.94, we can consult the standard normal table (available in Statistics books or on the Internet), and, specifically for this case, we need to consult the cumulative standard normal table (cumulative probability from
`\\ -\infty` to the value of z).

Here we have z = 2.94. The entry to consult the table is 2.9 (positive). Then, looking carefully the first row in the table, we need to find the column with value 0.04 (to have z = 2.94). The intersection of these two values "gives us" the cumulative probability for z = 2.94. Then,
`\\ P(z<2.94) = 0.99836`.

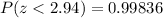This is also the cumulative probability for
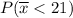`\\ P(\overline{x}<21)` (as we explained above, z is the standardized value for
`\\ \overline{x}`.)

However, we need to know
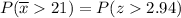`\\ P(\overline{x}>21) = P(z>2.94)`. Since

`\\ P(z<2.94) + P(z>2.94) = 1`

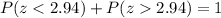
Then

`\\ P(z>2.94) = 1 - P(z<2.94)`

`\\ P(z>2.94) = 1 - 0.99836`

`\\ P(\overline{x}>21) = P(z>2.94) = 0.00164`

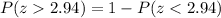
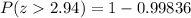
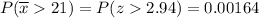
Therefore, "the probability that we will obtain a sample mean greater than 21" is 0.00164.