Answer:
0.85
Step-by-step explanation:
Given:-
- The diameter of the cylinder, d = 50 mm
- The compressive axial load, P = - 80KN
- The Poisson ratio of the material, v = 0.3
Find:-
- The ratio of axial strain when the cylinder is perfectly enclosed to when the radial expansion is free.
Solution:-
- We will first determine the axial stress ( σz ) due to the compressive axial loading ( P ).
- From definition, stress is defined as the ratio of loading ( P ) and the cross-sectional area ( A ) of the specimen under loading.
- Mathematically expressed as:
σz =
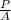
Where,
A: The cross sectional area of the cylinder
σz =

σz =
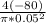
σz =

- Now we will state the stress-strain relationship for the axial strain in terms of stresses in cylindrical coordinate system.
εz = [ σz - v*(σl ) ] / E
εl = [ σl - v*(σz) ] / E
Where,
σl: The lateral stress
εl: The lateral strain
- Since, the cylinder is only subjected to axial loading the lateral stress ( σl = 0 ). The stress-strain relationship can be reduced down to:
εz = [ σz ] / E
εl = -[ v*σz ] / E
- We are told that in one case the cylinder is partially enclosed such that the lateral expansion is halved. So the lateral strain is also halved. We will use the lateral strain expression and multiply ( 1 / 2 ) on both sides:
[εl/2] = -[ v*σz ] / 2E
- For the law of isotropic medium to be maintained the total volume of the cylinder must remain constant. The amount by which the lateral strain is reduced the same amount adds up to to axial strain:
- So the new axial strain (εz') would be:
εz' = [ σz ] / E - [ v*σz ] / 2E
εz' = [ 2σz - v*σz ] / 2E
- Now take the ratio of ( εz' ) to ( εz ) as follows:
εz' / εz = ( [ 2σz - v*σz ] / 2E ) / ( σz / E )
εz' / εz = ( [ 2σz - v*σz ] / 2 ) / ( σz )
εz' / εz = ( [ 2 - v ] / 2 )
εz' / εz = ( 1 - v / 2 )
εz' / εz = ( 1 - 0.3 / 2 )
εz' / εz = 0.85