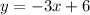Answer:
Explanation:
Coordinates are (0,6) and (1,3)
Slope =
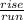
Slope =
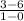
Slope = -3
Now, Finding b
Taking any Point
Point = (x,y) = (0,6)
So, x = 0, y = 6
Putting in slope-intercept form to find b
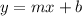
=> 6 = (-3)(0)+b
=> b = 6
Now Putting slope and b in the formula to get the required slope-intercept form.
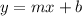
=>