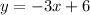Question

What is the equation in point-slope form of the line passing through (0,6) and (1,3)

Answer 1

Answer:
`y - 3 = -3(x - 1)`

Explanation:

You can start by finding the slope (m),
`(y1 - y2)/(x1 - x2)`:

`(y1 - y2)/(x1 - x2) = (6 - 3)/(0 - 1) = (3)/(-1) = -3.`

Now, plug the range and one points into the point-slope form equation,
`y - y1 = m(x - x1)`:

`y - y1 = m(x - x1)`

`y - 3 = -3(x - 1)`

Answer 2

`y = -3x+6`

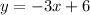
Explanation:

Coordinates are (0,6) and (1,3)

Slope =
`(rise)/(run)`

Slope =
`(3-6)/(1-0)`

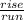
Slope = -3

Now, Finding b

Taking any Point

Point = (x,y) = (0,6)

So, x = 0, y = 6

Putting in slope-intercept form to find b

`y =mx+b`

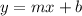
=> 6 = (-3)(0)+b

=> b = 6

Now Putting slope and b in the formula to get the required slope-intercept form.

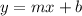
`y =mx+b`

=>
`y = -3x+6`