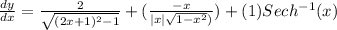Answer:
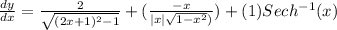
Explanation:
Step(i):-
Given function
 ....(i)
....(i)
we will use differentiation formulas
i) y = cos h⁻¹ (x)
Derivative of cos h⁻¹ (x)
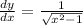
ii)
y = sec h⁻¹ (x)
Derivative of sec h⁻¹ (x)
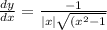
Apply U V formula
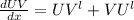
Step(ii):-
Differentiating equation (i) with respective to 'x'
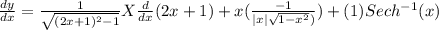
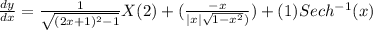
Conclusion:-