Question

Calculate the equivalent capacitance of the three series capacitors in Figure 12-1

Answer 1

The question is incomplete! Complete question along with answer and step by step explanation is provided below.

Question:

Calculate the equivalent capacitance of the three series capacitors in Figure 12-1

a) 0.01 μF

b) 0.58 μF

c) 0.060 μF

d) 0.8 μF

Answer:

The equivalent capacitance of the three series capacitors in Figure 12-1 is 0.060 μF

Therefore, the correct option is (c)

Step-by-step explanation:

Please refer to the attached Figure 12-1 where three capacitors are connected in series.

We are asked to find out the equivalent capacitance of this circuit.

Recall that the equivalent capacitance in series is given by

`$ (1)/(C_(eq)) = (1)/(C_(1)) + (1)/(C_(2)) + (1)/(C_(3)) $`

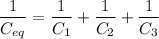
Where C₁, C₂, and C₃ are the individual capacitance connected in series.

C₁ = 0.1 μF

C₂ = 0.22 μF

C₃ = 0.47 μF

So the equivalent capacitance is

`$ (1)/(C_(eq)) = (1)/(0.1) + (1)/(0.22) + (1)/(0.47) $`

`$ (1)/(C_(eq)) = (8620)/(517) $`

`$ C_(eq) = (517)/(8620) $`

`$ C_(eq) = 0.0599 $`

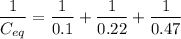
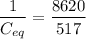
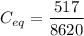
Rounding off yields

`$ C_(eq) = 0.060 \: \mu F $`

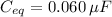
The equivalent capacitance of the three series capacitors in Figure 12-1 is 0.060 μF

Therefore, the correct option is (c)