Question

A sum of rs. 4000 is invested at a rate of 8% of compound intrest at 1st year and 10% at 2nd year. Find the sum of both the years. (Pls write the answer with steps and formulas). It's urgent

Answer 1

The sum after the second year is rs.4752

Explanation:

The interesting thing about solving for compound interest problems is understanding that the principal changes every year.

To solve this problem, we will break it into two years and solve for each year, so we can obtain the final sum to be paid at teh end of the second year.

Please note:

P = principal {the original sum invested}

R = rate of interest.

T= time required to pay back

Sum after the First Year:

Interest =
`(P * R * T)/(100)=(4000 * 8 * 1)/(100)=320`

Therefore his money after the first year is got by adding the interest of 320 to the initial principal which will givers. 4320.

After the first year, the money that will be used to calculate the new interest paid will be this rs.4320 obtained at the end of the first year.

Sum after the second Year

Interest =
`(P * R * T)/(100)=(4320 * 10 * 1)/(100)=432`

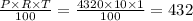
Sum = 4320+432 = rs.4752

Hence, the sum after the second year is rs.4752