Question

Field book of an land is given in the figure. It is divided into 4 plots . Plot I is a right triangle , plot II is an equilateral triangle, plot III is a rectangle and plot IV is a trapezium, Find the area of each plot and the total area of the field. ( use √3 =1.73)

Answer 1

Total area = 237.09 cm²

Explanation:

Given question is incomplete; here is the complete question.

Field book of an agricultural land is given in the figure. It is divided into 4 plots. Plot I is a right triangle, plot II is an equilateral triangle, plot III is a rectangle and plot IV is a trapezium, Find the area of each plot and the total area of the field. ( use √3 =1.73)

From the figure attached,

Area of the right triangle I =
`(1)/(2)(\text{Base})* (\text{Height})`

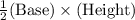
Area of ΔADC =
`(1)/(2)(\text{CD})(\text{AD})`

=
`(1)/(2)(√((AC)^2-(AD)^2))(\text{AD})`

=
`(1)/(2)(√((13)^2-(19-7)^2) )(19-7)`

=
`(1)/(2)(√(169-144))(12)`

=
`(1)/(2)(5)(12)`

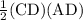
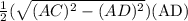
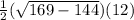
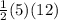
= 30 cm²

Area of equilateral triangle II =
`(√(3) )/(4)(\text{Side})^2`

Area of equilateral triangle II =
`(√(3))/(4)(13)^2`

=
`((1.73)(169))/(4)`

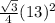
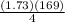
= 73.0925

≈ 73.09 cm²

Area of rectangle III = Length × width

= CF × CD

= 7 × 5

= 35 cm²

Area of trapezium EFGH =
`(1)/(2)(\text{EF}+\text{GH})(\text{FJ})`

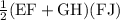
Since, GH = GJ + JK + KH

17 =
`\sqrt{9^(2)-x^(2)}+5+\sqrt{(15)^2-x^(2)}`

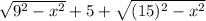
12 =
`√(81-x^2)+√(225-x^2)`

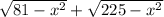
144 = (81 - x²) + (225 - x²) + 2
`√((81-x^2)(225-x^2))`

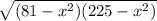
144 - 306 = -2x² +
`2√((81-x^2)(225-x^2))`

-81 = -x² +
`√((81-x^2)(225-x^2))`

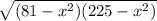
(x² - 81)² = (81 - x²)(225 - x²)

x⁴ + 6561 - 162x² = 18225 - 306x² + x⁴

144x² - 11664 = 0

x² = 81

x = 9 cm

Now area of plot IV =
`(1)/(2)(5+17)(9)`

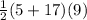
= 99 cm²

Total Area of the land = 30 + 73.09 + 35 + 99

= 237.09 cm²