The analytical derivations confirm that Equation 5, Equation 7, and Equation 6 represent valid trigonometric identity statements, as the left-hand sides simplify to match their respective right-hand sides.
The given trigonometric equations and show analytically that they represent trigonometric identity statements.
Equation 5:
![\[ \sin(x) \csc(x) + (\csc(x) + \sin(x) \sec^2(x)) = \sec^2(x) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/nonyel6f7q31hq46fcut.png)
We'll start by simplifying the left-hand side (LHS):
![\[ \text{LHS} = \sin(x) \csc(x) + \csc(x) + \sin(x) \sec^2(x) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/sm09zmo091z31p73u004.png)
Now, rewrite csc(x) as
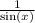 and
and
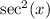 as
as
 :
:
![\[ \text{LHS} = (\sin(x))/(\sin(x)) + (1)/(\sin(x)) + (\sin(x))/(\cos^2(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bwbdektsv9cx5auokyoo.png)
Combine the fractions:
![\[ \text{LHS} = (\sin(x) + 1 + \sin(x))/(\sin(x)) \cdot (\cos^2(x))/(\cos^2(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/63gk04v2y9cmt9oohxgn.png)
Combine like terms:
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \cdot (\cos^2(x))/(\cos^2(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/h0pmpaumui2h2t3xb55a.png)
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xbbbeqbamzzz3jybhsn3.png)
Now, multiply the numerator and denominator by
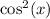 :
:
![\[ \text{LHS} = ((2\sin(x) + 1)\cos^2(x))/(\sin(x)\cos^2(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/h85gi0fkgjdfdypeklga.png)
Apply the trigonometric identity
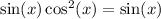 :
:
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xbbbeqbamzzz3jybhsn3.png)
![\[ \text{LHS} = 2 + (1)/(\sin(x)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jbjwrojqf40joyt5ilql.png)
Now, rewrite
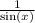 as csc(x):
as csc(x):
![\[ \text{LHS} = 2 + \csc(x) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pz93p0gu95xy1uq0tp2b.png)
Now, compare the simplified LHS with the given RHS
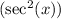 :
:
![\[ 2 + \csc(x) = \sec^2(x) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/z8vo8ux597gumafcu5te.png)
Hence, Equation 5 is satisfied.
Equation 7:
![\[ (1 + \sec(\theta))/(\tan(\theta)) + (\tan(\theta))/(1 + \sec(\theta)) = 2\csc(\theta) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/6huyk0rvrbxczdmz9r1c.png)
Start by finding a common denominator for the two fractions on the LHS, which is
 :
:
![\[ \text{LHS} = ((1 + \sec(\theta))^2 + \tan^2(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7piptr4ksx8q8hr64lo2.png)
Now, expand and simplify:
![\[ \text{LHS} = (1 + 2\sec(\theta) + \sec^2(\theta) + \tan^2(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3qspbfgmuf8d3rrpo38h.png)
Apply the trigonometric identity
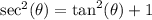 :
:
![\[ \text{LHS} = (2 + 2\sec(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xr33huxf9knco8r2yshp.png)
Combine like terms:
![\[ \text{LHS} = (2(1 + \sec(\theta)))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/w0mb2t5u4wypdqova8cm.png)
Now, cancel out common factors:
![\[ \text{LHS} = (2)/(\tan(\theta)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o336qnpilyl50kyntofi.png)
Recall that
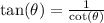 , so substitute this in:
, so substitute this in:
![\[ \text{LHS} = 2\cot(\theta) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/h6cb1w0b97t1go599nhy.png)
Finally, use the identity
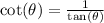 :
:
![\[ \text{LHS} = 2\cot(\theta) = 2\csc(\theta) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jdx0dlmzrqb9c8793zte.png)
Therefore, Equation 7 is satisfied.
Equation 6:
![\[ \sec^2(\theta) + \csc^2(\theta) = \sec^2(\theta)\csc^2(\theta) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/50yp42ezkdvchv8llr1g.png)
We'll start by using the definitions of
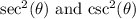 :
:
![\[ \text{LHS} = (1)/(\cos^2(\theta)) + (1)/(\sin^2(\theta)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p2jdcv3wj917d9wqerop.png)
Combine the fractions:
![\[ \text{LHS} = (\sin^2(\theta) + \cos^2(\theta))/(\sin^2(\theta)\cos^2(\theta)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8c680ps0b4vzzrz2v7td.png)
Apply the Pythagorean identity
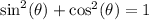 :
:
![\[ \text{LHS} = (1)/(\sin^2(\theta)\cos^2(\theta)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/z2mpycpwe6kqq1wkmgx3.png)
![\[ \text{LHS} = \sec^2(\theta)\csc^2(\theta) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xha6if8wqldsx8awygd9.png)
Therefore, Equation 6 is satisfied.
All three given equations represent trigonometric identity statements.