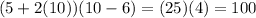Question

A square and rectangle have the same area. The length of the rectangle is 5cm more than twice the length of the side of the square. The width of the rectangle is 6cm less than the side of the square. Find the length of the side of the square.

Answer 1

10cm

Explanation:

First let's define variables a and x:

a = area of rectangle and square

x = side of square

Now let's create an equation to calculate a using the square and an equation to calculate a using the rectangle:

Using square:
`x^(2) =a`

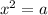
Using rectangle:
`(5+2x)(x-6)=a`

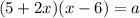
Now we want to solve for x so let's combine the equations since they are both equivalent to a

`(5+2x)(x-6)=x^(2)`

Simplify

`x^(2)-7x-30 = 0`

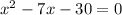
Solving this we get 10 and -3

Since it is impossible for a square to have a negative side value we can conclude that the value is 10cm

This can then be checked by plugging in 10 as x in our equations and seeing if we get the same a value:

Using square:
`10^(2) = 100`

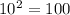
Using rectangle:
`(5+2(10))(10-6) = (25)(4) = 100`