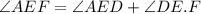Question

ABCD is a square Triangle DEF is equilateral Triangle ADE is isosceles AD= AE CDF is a straight line Show all your steps,calcutate the size of angle AEF

Answer 1

90 degrees

Explanation:

Triangle DEF is equilateral, therefore:

Angle DFE=Angle DEF =Angle EDF
`=60^\circ`

ABCD is a square, therefore:

`\angle CDA =90^\circ`

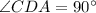
In the straight line CF

`\angle CDA + \angle ADE + \angle EDF =180^\circ`

`90^\circ+ \angle ADE +60^\circ=180^\circ\\\angle ADE=180^\circ-(90^\circ +60^\circ)\\\angle ADE=30^\circ`

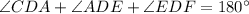
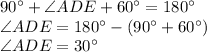
Recall that triangle ADE is an Isosceles triangle; therefore:

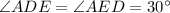`\angle ADE = \angle AED=30^\circ` (Base angles of an Isosceles Triangle)

We then have:

`\angle AEF=\angle AED+\angle DE.F`

`=30^\circ+60^\circ\\=90^\circ`