Question

George wants to invest his money such that he accumulates $10,000 after 3 and half years at a rate of 4% compounded monthly? How much money should he invest daily?

Answer 1

$8.77

Explanation:

Using the compound interest formula
`A = P(1+(r)/(n) )^(nt)`

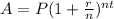
A = amount compounded (in $)

P = Principal (in $)

r = rate (in %)

t = time it takes to accumulate fund (in years)

n = time of compounding (in years)

Given P = $10,000, r = 4%, t = 3.5 years n = 1/12 years (since it is compounded monthly)

`A = 10000(1+(0.04)/((1/12)) )^((3.5)(1/12))\\A = 10000(1+0.48)^(0.2916)\\A = 10000(1.48)^(0.2916)\\A = 10000*1.12111\\A = 11,211.1`

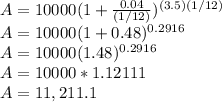
Amount he will compound after 3.5years will be $11,211.1.

Amount he should invest daily = Amount compounded/time taken (in days)

Since 3.5years ≈ 1278 days

Amount he should invest daily = $11,211.1/1278

Amount he should invest daily = $8.77