Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the

correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag
the item to the trashcan. Click the trashcan to clear all your answers.
Write the nth term of the following sequence in terms of the first term of the sequence.
1, 8, 15, 22, ...

Answer 1

`T_n = 7n -6`

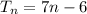
Explanation:

Given

Sequence: 1, 8, 15, 22, ...

Required

Find the nth term

The first step is to determine if the sequence is an arithmetic progression or a geometric progression.

It is arithmetic, if the difference between successive terms are equal

i.e.
`22 - 15 = 15 - 8 = 8 - 1 = 7`

The above expression represents the common difference, d

`d = 7`

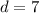
The nth term of an arithmetic sequence is calculated by

`T_n = a + (n - 1) d`

`Where\\ a = First\ Term = 1\\d = 7`

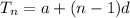
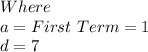
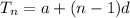`T_n = a + (n - 1) d` becomes

`T_n = 1 + (n - 1) *7`

`T_n = 1 + 7n -7`

`T_n = 7n +1-7`

`T_n = 7n -6`

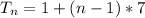
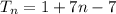
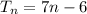
Hence, the nth term of the sequence is 7n - 6