The analytical derivations confirm that Equation 5, Equation 7, and Equation 6 represent valid trigonometric identity statements, as the left-hand sides simplify to match their respective right-hand sides.
The given trigonometric equations and show analytically that they represent trigonometric identity statements.
Equation 5:
![\[ \sin(x) \csc(x) + (\csc(x) + \sin(x) \sec^2(x)) = \sec^2(x) \]](https://img.qammunity.org/2023/formulas/mathematics/college/knx2ou9swwq71q7gndyc8ux9v4wfwjr2s5.png)
We'll start by simplifying the left-hand side (LHS):
![\[ \text{LHS} = \sin(x) \csc(x) + \csc(x) + \sin(x) \sec^2(x) \]](https://img.qammunity.org/2023/formulas/mathematics/college/9g0fzbghsod41s992a6w89p520s5228a9m.png)
Now, rewrite csc(x) as
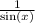 and
and
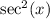 as
as
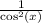 :
:
![\[ \text{LHS} = (\sin(x))/(\sin(x)) + (1)/(\sin(x)) + (\sin(x))/(\cos^2(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/30cq99j8p774brqwoei9xjwd7hgsubuem0.png)
Combine the fractions:
![\[ \text{LHS} = (\sin(x) + 1 + \sin(x))/(\sin(x)) \cdot (\cos^2(x))/(\cos^2(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/bun0i7mwsn537f6rkgdpc5e6qwb2z07vm8.png)
Combine like terms:
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \cdot (\cos^2(x))/(\cos^2(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/6ad6xf7js0nr6dznecssp4sq3h6h4nnxgq.png)
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/ld6cjqovcsd7m3vj17mx2a0ml8rc012uuq.png)
Now, multiply the numerator and denominator by
 :
:
![\[ \text{LHS} = ((2\sin(x) + 1)\cos^2(x))/(\sin(x)\cos^2(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/m0p9d8s05ia5p25k9pakq5tkh4p7e9es8u.png)
Apply the trigonometric identity
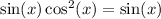 :
:
![\[ \text{LHS} = (2\sin(x) + 1)/(\sin(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/ld6cjqovcsd7m3vj17mx2a0ml8rc012uuq.png)
![\[ \text{LHS} = 2 + (1)/(\sin(x)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/amoksyjlv75hl2n6wv084233rpdwi9ps6q.png)
Now, rewrite
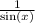 as csc(x):
as csc(x):
![\[ \text{LHS} = 2 + \csc(x) \]](https://img.qammunity.org/2023/formulas/mathematics/college/srr0u60v4a8qqn0g6120lp1s3rhd5f9exv.png)
Now, compare the simplified LHS with the given RHS
 :
:
![\[ 2 + \csc(x) = \sec^2(x) \]](https://img.qammunity.org/2023/formulas/mathematics/college/lyqu18cafhpzhny1sfvmno4tfeqw39gubc.png)
Hence, Equation 5 is satisfied.
Equation 7:
![\[ (1 + \sec(\theta))/(\tan(\theta)) + (\tan(\theta))/(1 + \sec(\theta)) = 2\csc(\theta) \]](https://img.qammunity.org/2023/formulas/mathematics/college/tlhbcyuakfa9o84im9zy93zu1tu1uhogjm.png)
Start by finding a common denominator for the two fractions on the LHS, which is
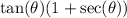 :
:
![\[ \text{LHS} = ((1 + \sec(\theta))^2 + \tan^2(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/2023/formulas/mathematics/college/tbji00krelrre2dpk2wxglxw1iwnyladtg.png)
Now, expand and simplify:
![\[ \text{LHS} = (1 + 2\sec(\theta) + \sec^2(\theta) + \tan^2(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/2023/formulas/mathematics/college/w9hi6v785mwg06hyvgxsmj7krkkqyr49qq.png)
Apply the trigonometric identity
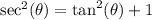 :
:
![\[ \text{LHS} = (2 + 2\sec(\theta))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/2023/formulas/mathematics/college/71d995272mq24v4rwq8megi4pzmv8lirb9.png)
Combine like terms:
![\[ \text{LHS} = (2(1 + \sec(\theta)))/(\tan(\theta)(1 + \sec(\theta))) \]](https://img.qammunity.org/2023/formulas/mathematics/college/fa4yhgdlml35gkfs0hap391liu3v9lx1d1.png)
Now, cancel out common factors:
![\[ \text{LHS} = (2)/(\tan(\theta)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/paaef0rtr6rughecton17n2mvv85aidzho.png)
Recall that
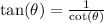 , so substitute this in:
, so substitute this in:
![\[ \text{LHS} = 2\cot(\theta) \]](https://img.qammunity.org/2023/formulas/mathematics/college/e5y623shd3zjnn5ae6b5yohq1itjbqfexx.png)
Finally, use the identity
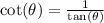 :
:
![\[ \text{LHS} = 2\cot(\theta) = 2\csc(\theta) \]](https://img.qammunity.org/2023/formulas/mathematics/college/anbcxxa5w3d1r4l0yd15uyprj46rw6o3kt.png)
Therefore, Equation 7 is satisfied.
Equation 6:
![\[ \sec^2(\theta) + \csc^2(\theta) = \sec^2(\theta)\csc^2(\theta) \]](https://img.qammunity.org/2023/formulas/mathematics/college/o9nuow411rjyj5o127hf3g1a25j5iy98pb.png)
We'll start by using the definitions of
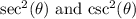 :
:
![\[ \text{LHS} = (1)/(\cos^2(\theta)) + (1)/(\sin^2(\theta)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/ny8r9bbn0rbmofdfh3suarxnudr8mken2r.png)
Combine the fractions:
![\[ \text{LHS} = (\sin^2(\theta) + \cos^2(\theta))/(\sin^2(\theta)\cos^2(\theta)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/j037a78brzuanpyohzb1gppcmsztdmql7m.png)
Apply the Pythagorean identity
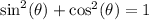 :
:
![\[ \text{LHS} = (1)/(\sin^2(\theta)\cos^2(\theta)) \]](https://img.qammunity.org/2023/formulas/mathematics/college/fu69rttajuh9gryw48fivhnhv279rovt5m.png)
![\[ \text{LHS} = \sec^2(\theta)\csc^2(\theta) \]](https://img.qammunity.org/2023/formulas/mathematics/college/5mx6irrer48mj8i5hdc1rq0is69o24g1bw.png)
Therefore, Equation 6 is satisfied.
All three given equations represent trigonometric identity statements.