Question

The drama club was selecting which carnival booths to sponsor at the fall carnival from a list of nine. How many different ways can they choose three booths from a selection of nine? A 42 B 84 C 508 D 814

Answer 1

B. 84 is correct.

I did the quiz.

Answer 2

Option B

Explanation:

Here we have to apply " combination and permutation. " It is given that the drama club had to choose three booths from a selection of 9, considering the possible ways to choose so. This is a perfect example of combination. In nCr, n corresponds to 9, respectively r corresponds to 3.

`\mathrm{n\:choose\:r},\\nCr=(n!)/(r!\left(n-r\right)!),\\\\(9!)/(3!\left(9-3\right)!) =\\(9!)/(3!\cdot \:6!) =\\\\(9\cdot \:8\cdot \:7)/(3!) =\\(504)/(6) =\\\\84\\\\Solution = Option B`

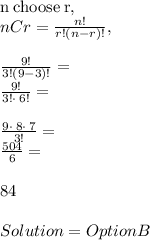
Hope that helps!