Question

`(√(3) )/(√(8) )`

Answer 1

Step-by-step explanation:

√8/√3

√8≈2.83

√3≈1.73

Therefore your answer should be ABOUT

2.83/1.73

Simplify to about 1.64

Answer 2

Step-by-step explanation:

This is a radical (it contains square roots). A known rule of algebraic expressions is that you can NEVER have a square root in the denominator. Therefore, we must go through a process called rationalization. This process is shown below:

`(2√(2) )/(√(3) ) *(√(3) )/(√(3) )`

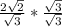
First, you want to simplify the radical
`√(8)`. This is quite easy. Firstly, divide the square root by the smallest prime number that you can. This is 2 (dividing by 1 is pointless). This gives us
`(√(8) )/(2)`. Dividing this will give us
`√(2)`. This is because we have to split up the radical on top first to give us
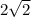`2√(2)`. Then, dividing by 2 leaves us with an isolated
`√(2)`.

Then, we multiply by the radical in the denominator in order to eliminate the radical in the denominator (it sounds odd, but I will demonstrate it so it makes sense). This gives us
`(2√(2) )/(√(3) ) *(√(3) )/(√(3) )`.

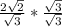This next step is doing simple multiplication. We always do cross-multiplication in this step because it is easier to demonstrate. Therefore, we are going to have a little bit of simplifying to do (don't worry, I have worked this all out for you).

`2√(2) *√(3)` =
`2*(√(2)*√(3) )`

`√(2) * √(3) = √(2*3)`

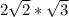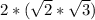
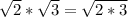
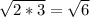`√(2*3) = √(6)` (Now, reintroduce the coefficient of 2)

⇒
`2√(6)`

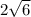
The denominators cancel out and simply become
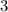`3` (multiplying one square root by another is the same operation as multiplying the two numbers together and then taking the square root of them). This leaves us with
`(2√(6) )/(3)`.

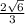Then, we can either simplify this answer into a decimal or we can leave it as is (this is our final answer). Simply use a calculator and simplify the result if you need to in order to get
`(2√(6) )/(3) = 1.63299`.