Answer:
P( x < 8) = 0.0344
Explanation:
Step(i):-
Given 'n' = 20 and 'p' = 0.60
Mean of the binomial distribution = n p
μ = n p = 20 × 0.60 = 12
Mean 'μ' = 12
Standard deviation of the binomial distribution =
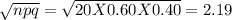
Standard deviation σ = 2.19
Step(ii):-
Let 'X' be the random variable of normal distribution
Let 'x' = 8
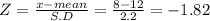
P( x < 8) = P( Z< -1.82)
= 1- P( Z>1.82) (∵ A(-1.82) = A(1.82)
= 1 - (0.5 + A( 1.82))
= 0.5 - A (1.82)
= 0.5 - 0.4656
= 0.0344
Conclusion:-
P( x < 8) = 0.0344