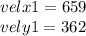Answer:
28.8 degrees bearing above from the east.
Explanation:
Given :
Direction =30 degrees
Speed =724 km/hr
Suppose x1, y1 be the velocity bearing in the east at the 30 degree
so x1 velocity = 724 cos 30 degree
y1 velocity = 724 sin 30 degree
As mention in the question the wind speed adding another 32 to the x1 speed.
Hence the resultant speed is