![\huge \underbrace \mathfrak \red{Answer}]()
To find :-
To get the value of 'di in figure 3 and 4.
Figure 3
- According to the figure, we know that it is a quadrilateral.
- It's all sides are at 90°.
- So we can assume that it can be rectangle.
- In the figure, length of one side is given and area of figure is given and we have the length of another side.
Solution :-
Area of rectangle = length × width
area = 108 ft², length = 12 ft, width = x
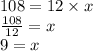
- Therefore, the value of x in this figure is 9 ft.

Figure 4
- According to figure, we finds out that it is quadrilateral as it has 4 sides.
- It has all parallel sides.
- We can assume that it is parallelogram as the sides which are facing each other are parallels.
- And here value of one side is given which is base and area is given, we have to find here is height.
Solution :-
Area of parallelogram = base × height
Area = 96 cm², base = 16 cm, height = x
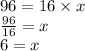
- Therefore, the value of x is 6 cm.