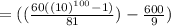Question

Find the sum of the digits of the number 6+66+666+6666 + ... +666...66, where the last number contains 100 digits.

Answer 1

Sum of the digits of the number

`= (((60((10)^(100)-1) )/(81)) - (600)/(9) )`

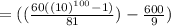
Explanation:

Step(i):-

Given series

6+66+666+6666 + ... +666...66 up to 100 digits

Taking common '6'

6 ( 1 + 11 +111+ 1111+1111+.................11111....11 100 digits)

Multiply '9' and divisible by'9'

`(6)/(9) X9( 1+11 +111 +1111 +1111+ ..........11111..up to .100 digits )`

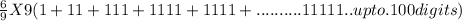
Multiply inside '9'

`(6)/(9)( 9+99 +999 +9999 +.....+ ..........9999..up to .100 digits )`

`(6)/(9)( (10-1)+(100-1)+(1000-1) +(10,000-1)+.....+ ............up to .100 digits )`

`(6)/(9)( (10)+(100)+(1000) +(10,000)+.....+ ............up to .100 digits ) - ( 1+1+1+1+........up to 100 digits)`

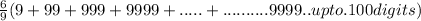
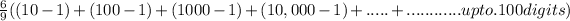
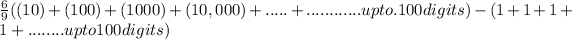
Step(ii):-

we know that sum of geometric series

`S_(n) = (a(r^(n)-1) )/(r-1)`

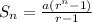
we know that

a + a + a+........n terms = n a

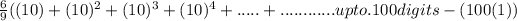`(6)/(9)( (10)+(10)^(2) +(10)^(3) +(10)^4+.....+ ............up to .100 digits - (100(1))` ....(i)

The sum of the 100 digits in geometric series

`S_(100) = (10((10)^(100)-1) )/(10-1)`

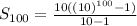
Now the equation (i)

The sum of the digits of the number

`= (6)/(9) (((10((10)^(100)-1) )/(10-1)) - 100)`

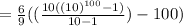
Final answer :-

Sum of the digits of the number

`= (((60((10)^(100)-1) )/(81)) - (600)/(9) )`