Question

Given: ∆ABC, m∠C = 90° CB = 8, m∠B = 38º Find the area of a circumscribed circle. Find the area of the inscribed circle.

Answer 1

Circumscribed circle: Around 80.95

Inscribed circle: Around 3.298

Explanation:

Since C is a right angle, when the circle is circumscribed it will be an inscribed angle with a corresponding arc length of 2*90=180 degrees. This means that AB is the diameter of the circle. Since the cosine of an angle in a right triangle is equivalent to the length of the adjacent side divided by the length of the hypotenuse:

`\cos 38= (8)/(AB) \\\\\\AB=(8)/(\cos 38)\approx 10.152`

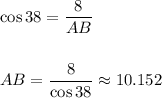
To find the area of the circumscribed circle:

`r=(AB)/(2)\approx 5.076 \\\\\\A=\pi r^2\approx 80.95`

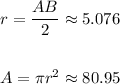
To find the area of the inscribed circle, you need the length of AC, which you can find with the Pythagorean Theorem:

`AC=√(10.152^2-8^2)\approx 6.25`

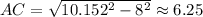
The area of the triangle is:

`A=(bh)/(2)=(8\cdot 6.25)/(2)=25`

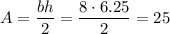
The semiperimeter of the triangle is:

`(10.152+6.25+8)/(2)\approx 24.4`

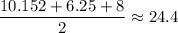
The radius of the circle is therefore
`(25)/(24.4)\approx 1.025`

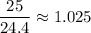
The area of the inscribed circle then is
`\pi\cdot (1.025)^2\approx 3.298`.

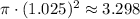Hope this helps!