Question

-1/2 divided by 1 3/4 as a fraction in simplest form

Answer 1

`\Large\textsf{\textbf{Answer\;:}}}`

`\large\textsf{refer\:to\:the\:`

`\Large\textsf{\textbf{Calculations\::}}`

`-\displaystyle(1)/(2) :1(3)/(4)`

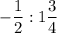
First , convert the mixed number (the fraction we are dividing by in the given maths problem) into an improper fraction .

Multiply the whole part (1) times the denominator (4) and add the numerator . The result is the numerator of our fraction , and the denominator stays the same .

So now our maths problem looks as follows :

`-\displaystyle(1)/(2) :(7)/(4)`

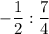
Now turn the fraction you are dividing by over :

`-\displaystyle(1)/(2) *(4)/(7)`

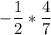
Now multiply the numerator of the first fraction times the numerator of the second fraction :

4

Perform the same operation with the denominators :

-4/14

So the result is :

`-\displaystyle(4)/(14)`

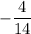
Since the above fraction is not in it's simplest form , we divide the top and bottom by 2 (a common factor of both 4 and 14) :

`-\displaystyle(2)/(7)`

`\footnotesize\textsf{hope\:helpful~}`