Answer:
x: C
y: A
z:
Explanation:
In a 45-45-90 triangle, the hypotenuse is larger than either of the legs by a factor of
 . The length of x is therefore:
. The length of x is therefore:

In a 30-60-90 triangle, the longer leg is larger than the shorter leg by a factor of
 . Therefore:
. Therefore:
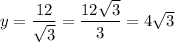
The hypotenuse of the 30-60-90 triangle is twice larger than the smallest leg, so it has a length of
 .
.
By the pythagorean theorem, you can find z+y:
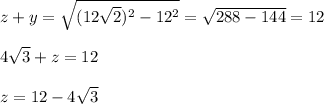
Hope this helps!