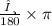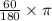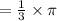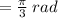Question

Angles A and B are supplementary. The measure of angle A is twice the measure of angle B. What is the measure of angle B in radians?

Answer 1

The answer is π/3 rad.

Step-by-step explanation:

Given that ∠A and ∠B are supplementary angles so when both angles are added up, it will form 180°. ∠A is twice the measure of ∠B :

`let \: B = θ \\ let \: A = 2B = 2θ`

`2θ + θ = 180`

`3θ = 180`

`θ = 180 / 3`

`θ = 60`

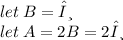
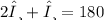
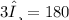
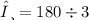
Next, you have to convert 60° into radian by using the formula :

`(θ)/(180) * \pi`

`(60)/(180) * \pi`

`= (1)/(3) * \pi`

`= (\pi)/(3) \: rad`