Question

What's the equation of the line that's a perpendicular bisector of the segment connecting C (6, –12) and D (10, –8)? answers: A) y = –x – 2 B) y = x + 2 C) y = –1∕2x – 2 D) y = 2x – 6

Answer 1

y=-x-2

letter A

Answer 2

A

Explanation:

Perpendicular bisector of a line divides the line into 2 equal parts and it is perpendicular to the line.

First let's find the midpoint of CD. The point is where the perpendicular bisector will cut through the line.

midpoint=
`( (x1 + x2)/(2) , (y1 + y2)/(2) )`

Thus, midpoint of CD

`= ( (6 + 10)/(2) , ( - 12 - 8)/(2) ) \\ = ( (16)/(2) , ( - 20)/(2) ) \\ = (8, - 10)`

Gradient of line CD

`= (y1 - y2)/(x1 - x2) \\ = ( - 12 - ( - 8))/(6 - 10) \\ = ( - 12 + 8)/( - 4) \\ = ( - 4)/( - 4) \\ = 1`

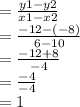
The product of the gradients of perpendicular lines is -1.

gradient if perpendicular bisector(1)= -1

gradient of perpendicular bisector= -1

y=mx +c, where m is the gradient and c is the y-intercept.

y= -x +c

Subst a coordinate to find c.

Since the perpendicular bisector passes through the point (8, -10):

When x=8, y= -10,

-10= -8 +c

c= -10 +8

c= -2

Thus, the equation of the perpendicular bisector is y= -x -2.