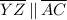Question

Given that points A, B, and C are the midpoints of their respective sides, which of the following is true about the figure? ANSWERS: A) ∠Y ≅ ∠Z B) ∠X ≅ ∠ACB C) || D) ||

Answer 1

Answer:ΔBCZ ≅ ΔYAB

Step-by-step explanation: since we know the midpoint are <ABC we can see the that answer is correct.

Answer 2

The correct option is;

`\overline{YZ}\left | \right | \overline{AC}`

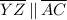
Explanation:

The dimensions given are;

YX = 2 × AX (A = midpoint of YX)

ZX = 2 × CX (C = midpoint of ZX)

∠X and ∠X are congruent (Reflexive property)

Therefore, triangle XAC is similar to triangle XYZ (SAS similarity theorem)

Since ∠XYZ = ∠XAC segments YZ and AC are parallel from having equal angle on the same side of the transversal YX

Therefore the correct option should be;

`\overline{YZ}\left | \right | \overline{AC}`