Question

FAST PLEASE 50 POINTS :D

What is the area of a rectangle with vertices (Negative 8, Negative 2), (Negative 3, Negative 2), (Negative 3, Negative 6), and (Negative 8, Negative 6)? square units

Answer 1

20 units ^2

Explanation:

The vertices are ( -8,-2) (-3,-2) (-3,-6) (-8,-6)

The sides are parallel

The lengths are *2- to -6 = 4 units

and -8 to -3 = 5 units

4*5 = 20 units ^2

Answer 2

Area = 20 units²

Explanation:

Let A(-8,-2), B(-3,-2), C(-3,-6) and D(-8,-6) so that the rectangle becomes ABCD.

=> Since it's a rectangle it will have two opposite sides equal.

So, let's find the length of any two sides (as length and width) by Distance Formula.

Distance Formula =
`√((x2-x1)^2+(y2-y1)^2)`

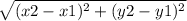
Side AB:

|AB| =
`√((-3+8)^2+(-2+2)^2)`

|AB| =
`√(5^2)`

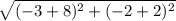
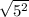
|AB| = 5

Side BC:

|BC| =
`√((-3+3)^2+(-6+2)^2)`

|BC| =
`√(16)`

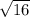
|BC| = 4

Now, Area:

Area of the rectangle = Length * Width

Area = 4 * 5

Area = 20 units²