Answer:
Explanation:
Hello,
as cosx+sinx=k we can write that

and we know that
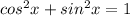
so
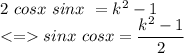
which is the answer to the question 2
Now, let s estimate

so
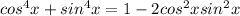
We use the previous result to write
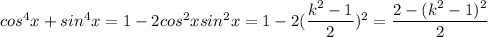
and we know that
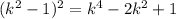
so

this is the answer to the first question
finally, let s estimate
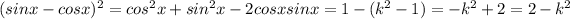 so
so
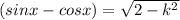
and this is the answer to the last question
do not hesitate if you need further explanation
hope this helps