Question

Answer the question ​

Answer 1

Hey there!

------------------------------------------------------------------

ANGLES

We see that the angle measure of angle VBC is 23 degrees. If you add this with the 90 degree angle of angle VCB, we can see that the measure of angle BVC is 67 degrees because sum of the interior angles of a triangle is 180 degrees.

------------------------------------------------------------------

SOLVING FOR BC

Let's solve for some sides to to help us to to AC. We have that VC is 30 cm and is a leg of the triangle VCB. We see that the angle VBC is 23 degrees. Let's solve for CB. From the angle VBC, VC is the opposite side and CB is the adjacent. So, we see that the tangent of 23 is equal to 30 divided by whatever CB is. We can rearrange this problem to plug into our calculators.

`tan23=(30)/(CB) \\CB(tan23)=30\\CB=(30)/(tan23)`

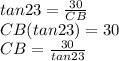
If you use your calculator, you see that CB is equal to about 71 cm.

------------------------------------------------------------------

SOLVING FOR AC

Now, let's look at the triangle BCA. We see that the angle BAC is 30 degrees. The side AC is the adjacent, and CB, 71 cm, is opposite. Tangent is opposite over adjacent, so we will use this.

`tan30=(71)/(AC) \\AC(tan30)=71\\AC=(71)/(tan30)`

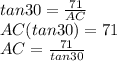
We plug this in and we get about 123 cm.

Therefore, the answer is A. 123 cm.

I hope that this helps! Have a wonderful day!

------------------------------------------------------------------