Question

Mr. Williams is driving on a highway at an average speed of 50 miles per hour. His destination is 100 miles away. The

equation d - 100 - 50t gives the distance d (in miles) that he has left to travel as a function of the time t (in hours) that h
been driving. Write and interpret the inverse of this function (2 points per part).

Answer 1

`d=2-(t)/(50)`.

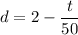Initial distance is 2 miles and the average speed is
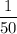`(1)/(50)` miles per hour. So, d is distance in miles that he has left to travel as a function of the time t (in hours).

Explanation:

It is given that, mr. Williams is driving on a highway at an average speed of 50 miles per hour. His destination is 100 miles away.

The equation of distance is

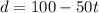`d=100-50t` ...(1)

where, d is distance in miles that he has left to travel as a function of the time t (in hours).

We need to find the inverse of the above function.

To find the inverse, interchange variables in (1) and isolate variable d on one side.

`t=100-50d`

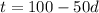
Subtract 100 from both sides in equation (1).

`t-100=-50d`

Divide both sides by -50.

`(t-100)/(-50)=(-50d)/(-50)`

`(t)/(-50)+2=d`

`2-(t)/(50)=d`

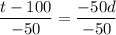
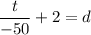
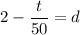
So, the inverse function is
`d=2-(t)/(50)`.

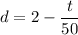Here, the initial distance is 2 miles and the average speed is
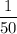`(1)/(50)` miles per hour. So, d is distance in miles that he has left to travel as a function of the time t (in hours).