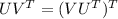Question

View vectors in set of real numbers R Superscript n as n times 1 matrices. For u and v in set of real numbers R Superscript n ​, the matrix product Bold u Superscript Upper T Baseline Bold v is a 1 times 1 ​matrix, called the scalar​ product, or inner​ product, of u and v. It is usually written as a single real number without brackets. The matrix product Bold uv Superscript Upper T is an n times n ​matrix, called the outer product of u and v. Suppose u and v are in set of real numbers R Superscript n . How are Bold u Superscript Upper T Baseline Bold v and Bold v Superscript Upper T Baseline Bold u ​related? How are Bold uv Superscript Upper T and Bold vu Superscript Upper T ​related?

Answer 1

The inner product holds the commutative property while the outer product does not hold. This indicates that
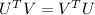`U^TV=V^TU` and
`UV^T=(VU^T)^T`

Explanation:

For any two vectors, U and V, given as,

`U=\left[\begin{array}{c}a1\\a2\\a3\\.\\.\\an\end{array}\right] \\V=\left[\begin{array}{c}b1\\b2\\b3\\.\\.\\bn\end{array}\right]`

Here a1,a2,a3,b1,b2 and b3,.....,an,bn are real numbers

The products are given as

`U^TV=\left[\begin{array}{cccccc}a1&a2&a3&.&.&an\end{array}\right] \left[\begin{array}{c}b1\\b2\\b3\\.\\.\\bn\end{array}\right]\\U^TV=\left[\begin{array}{c}a1*b1+a2*b2+a3*b3+....+an*bn\end{array}\right]`

`V^TU=\left[\begin{array}{cccccc}b1&b2&b3&.&.&bn\end{array}\right] \left[\begin{array}{c}a1\\a2\\a3\\.\\.\\an\end{array}\right]\\V^TU=\left[\begin{array}{c}b1*a1+b2*a2+b3*a3+....+bn*an\end{array}\right]`

From this, it is clear that the inner product or the scalar product of two vectors U, V is commutative i.e

`U^TV=V^TU`

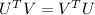
Now for the outer or vector product

`UV^T=\left[\begin{array}{c}a1\\a2\\a3\\.\\.\\an\end{array}\right]\left[\begin{array}{cccccc}b1&b2&b3&.&.&bn\end{array}\right] \\UV^T=\left[\begin{array}{cccccc}a1*b1&a1*b2&a1*b3&.&.&a1*bn\\a2*b1&a2*b2&a2*b3&.&.&a2*bn\\a3*b1&a3*b2&a3*b3&.&.&a3*bn\\.&.&.&.&.&.\\.&.&.&.&.&.\\an*b1&an*b2&an*b3&.&.&an*bn\end{array}\right]\\UV^T=\left[\begin{array}{cccccc}a1b1&a1b2&a1b3&.&.&a1bn\\a2b1&a2b2&a2b3&.&.&a2bn\\a3b1&a3b2&a3b3&.&.&a3bn\\.&.&.&.&.&.\\.&.&.&.&.&.\\anb1&anb2&anb3&.&.&anbn\end{array}\right]`

`VU^T=\left[\begin{array}{c}b1\\b2\\b3\\.\\.\\bn\end{array}\right]\left[\begin{array}{cccccc}a1&a2&a3&.&.&an\end{array}\right] \\VU^T=\left[\begin{array}{cccccc}b1*a1&b1*a2&b1*a3&.&.&b1*an\\b2*a1&b2*a2&b2*a3&.&.&b2*an\\b3*a1&b3*a2&b3*a3&.&.&b3*an\\.&.&.&.&.&.\\.&.&.&.&.&.\\bn*a1&bn*a2&bn*a3&.&.&bn*an\end{array}\right]\\VU^T=\left[\begin{array}{cccccc}b1a1&b1a2&b1a3&.&.&b1an\\b2a1&b2a2&b2a3&.&.&b2an\\b3a1&b3a2&b3a3&.&.&b3an\\.&.&.&.&.&.\\.&.&.&.&.&.\\bna1&bna2&bna3&.&.&bnan\end{array}\right]`

From this, it is clear that the outer product or the vector product of two vectors U, V is not commutative i.e

`UV^T\\eq VU^T`

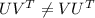
However, it is evident that

`UV^T=(VU^T)^T`