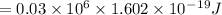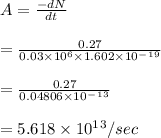Question

A person with lymphoma receives a dose of 45 Gy in the form of γ radiation during a course of radiotherapy. Most of this dose is absorbed in 18 g of cancerous lymphatic tissue. (a) How much energy is absorbed by the cancerous tissue? (b) If this treatment consists of five 20 minute sessions per week over the course of 5 weeks and just 1% of the γ photons in the γ ray beam are absorbed, what is the power of the γ ray beam? (c) If the γ ray beam consists of just 0.5% of the γ photons emitted by the γ source, each of which has energy of 0.03MeV, what is the activity (in Ci) of the γ ray source?

Answer 1

Step-by-step explanation:

a) Energy absorbed by cancerous tissue E = R x M

R is the radiation dosage

M is the mass of the lymphatic

Energy absorbed by cancerous tissue

`=45*18*10^-^3J\\\\=810*10^-^3J`

b) If only 1% of the total energy Et is absorbed over 20min session for 5 weeks = E

And the time of the period of the course is t = 20 x 5 = 100 min

E = 0.01Et

Total energy of gamma ray beam

Et = E x 100

= 810 x 10⁻³ x 100

= 8100J

Power of gamma ray beam is P

`P=(Et)/(t) \\\\=(8100J)/(100*60) \\\\=0.0135W`

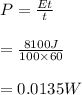
c) The total activity

`A=(-dN)/(dt) = dN decays/unit\ time`

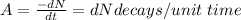
The Number of decays dN = Es Total energy emitted at sourse per seconds / energy emitted per day

`dN=( Es)/( 0.03Mev)`

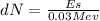
The Energy source Es per seconds = 0.05Ps

P= 0,0135W

The Power emitted at source

`Ps = (0.0135)/(0.05) \\\\=0.27W`

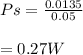
The Energy emitted per decay = 0.03MeV

`=0.03*10^6*1.602*10^-^1^9J`

`A=(-dN)/(dt) \\\\=(0.27)/(0.03*10^6*1.602*10^-^1^9) \\\\=(0.27)/(0.04806*10^-^1^3) \\\\=5.618*10^1^3/sec`