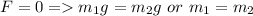Answer:
Step-by-step explanation:
Consider another special case in which the inclined plane is vertical (θ=π/2). In this case, for what value of m1 would the acceleration of the two blocks be equal to zero
F - Force
T = Tension
m = mass
a = acceleration
g = gravitational force
Let the given Normal on block 2 = N
and

and the tension in the given string is said to be

When the acceleration
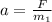
for the said block 1.
It will definite be zero only when Force is zero , F=0.
Here by Force, F
I refer net force on block 1.
Now we know
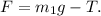
It is known that if the said
 ,
,
then Tension
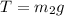
![[since \sin(\pi/2) = 1]](https://img.qammunity.org/2021/formulas/physics/college/qi0tth4k48w00gtsy2vastv13nydigniqr.png) ,
,
Now making
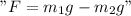
So If we are to make Force equal to zero