Question

Blood flows through a section of a horizontal artery that is partially blocked by a deposit along the artery wall. What is the speed of the blood in the partially blocked region

Answer 1

The question is incomplete. Here is the complete question.

Blood flows through a section of a horizontal artery that is partially blocked by a deposit along the artey wall. As a hemoglobin molecule moves from the narrow region into the wider region, its speed changes from v2 = 0.800 m/s to v1 = 0.411 m/s. What is the change in pressure, P1 - P2, that it experiences? The density of the blood is 1060 kg/m³.

Answer: P1 - P2 = 250 Pa.

Step-by-step explanation: The Bernoulli's Theorem states that the total mechanical energy of a flowing fluid (liquid or gas), comprising the energy associated with fluid pressure, the gravitational potential energy of elevation and the kinetic energy of fluid motion remains constant. In other words, if a fluid is moving horizontally, a decrease in pressure results in a increase of velocity.

Mathematically speaking:

`(v^2)/(2) + gh + (p)/(density) = cte`

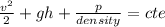
In the terms of the question:

`(v_1^(2))/(2) + (P1)/(density) = (v_2^(2))/(2) + (P2)/(density)`

`(P1)/(density) - (P2)/(density) = (1)/(2)(v_2^(2) - v_1^(2))`

P1 - P2 =
`(density)/(2)(v_2^(2) - v_1^(2))`

P1 - P2 =
`(1060)/(2)(0.8^(2) - 0.411^(2))`

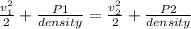
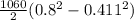
P1 - P2 = 250

The change in pressure experienced is 250 Pa.