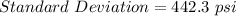Question

Compute the range and sample standard deviation for strength of the concrete​ (in psi).

3920​, 4090​, 3300​, 3100​, 2940​, 3830​, 4090​, 4030

The range is

1150 psi.

sequals

nothing psi​ (Round to one decimal place as​ needed.)

Answer 1

`Range = 1150\ psi`

`Standard\ Deviation = 442.3\ psi`

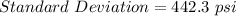
Step-by-step explanation:

Given

3920​, 4090​, 3300​, 3100​, 2940​, 3830​, 4090​, 4030

Required

- Determine the Range

- Determine the Standard Deviation

Calculating the Range...

The Range is calculated using the following formula;

`Range = Highest\ Strength - Least\ Strength`

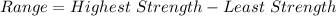
From the given data;

`Highest\ Strength = 4090\\ Least\ Strength = 2940`

Hence,

`Range = 4090 - 2940\\\\Range = 1150\ psi`

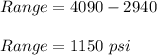
Calculating the Standard Deviation...

Start by calculating the mean

`Mean = (\sum x)/(n)`

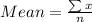
Where x->3920​, 4090​, 3300​, 3100​, 2940​, 3830​, 4090​, 4030

n = 8

`Mean = (3920 + 4090 + 3300 + 3100+ 2940+ 3830+ 4090+4030)/(8)`

`Mean = (29300)/(8)`

`Mean = 3662.5`

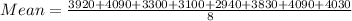
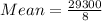
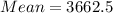
Subtract the mean from each observation

`3920​ - 3662.5 = 257.5\\4090​ - 3662.5 = 427.5\\3300 - 3662.5 = -362.5\\3100 - 3662.5 = -562.5\\2940 - 3662.5 = -722.5\\3830 - 3662.5 = 167.5\\4090 - 3662.5 = 427.5\\4030 - 3662.5 = 367.5`

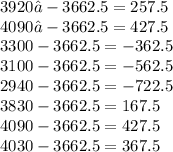
Square the result of the above

`257.5^2 =66,306.25\\427.5^2 =182,756\\-362.5^2 =131,406.25\\-562.5^2 =316,406.25\\-722.5^2 =522,006.25\\167.5^2 =28,056.25\\427.5^2 =182,756.25\\367.5^2 =135,056.25`

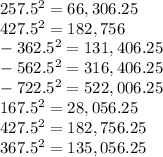
Add the above results together

`66,306.25+182,756+131,406.25+316,406.25+522,006.25+28,056.25+182,756.25+135,056.25 = 1564749.75`

Divide by n

`(1564749.75)/(8) = 195593.71875`

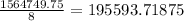
Take Square root of the above result to give standard deviation

`SD = √(195593.71875)`

`SD = 442.259786494`

`SD = 442.3\ psi\ (Approximated)`

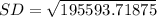
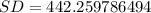
Hence,

`Range = 1150\ psi`

`Standard\ Deviation = 442.3\ psi`