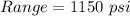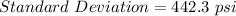Answer:
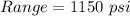
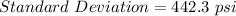
Step-by-step explanation:
Given
3920, 4090, 3300, 3100, 2940, 3830, 4090, 4030
Required
- Determine the Range
- Determine the Standard Deviation
Calculating the Range...
The Range is calculated using the following formula;
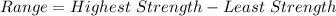
From the given data;
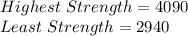
Hence,
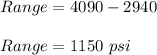
Calculating the Standard Deviation...
Start by calculating the mean
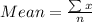
Where x->3920, 4090, 3300, 3100, 2940, 3830, 4090, 4030
n = 8
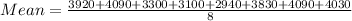
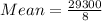
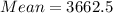
Subtract the mean from each observation
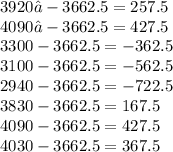
Square the result of the above
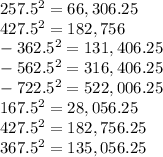
Add the above results together
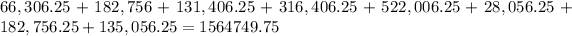
Divide by n
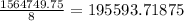
Take Square root of the above result to give standard deviation
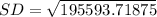
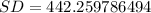
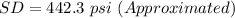
Hence,