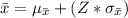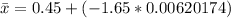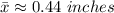Question

A tire manufacturer is measuring the margin of error in the thickness of their tires to make sure it is within safety limits. Overall, the tires' thickness is normally distributed with a mean of 0.45 inches and a standard deviation of 0.05 inches. What thickness separates the lowest 5% of the means from the highest 95% in a sample size of 65 tires

Answer 1

Z = -1.65

`\bar x \approx 0.44 \ inches`

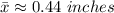
Explanation:

The main objective is to compute the data for the Z value and determine the
`\bar x` of the sample distribution

Given that;

the tires' thickness is normally distributed with a mean μ = 0.45 in

standard deviation σ = 0.05 in

sample size = 65 tires

Also; we are being told that the thickness separates the lowest 5% of the means from the highest 95%

∴

P(Z < Z) =0.05

From the Z- table

P(Z < -1.645) = 0.05

Z = -1.65

Similarly;

Let consider
`\bar x` to be the sample mean;

Then:

mean
`(\mu_(\bar x)) = \mu = 0.45`

standard deviation
`(\sigma_(\bar x) ) = (\sigma)/(√(n))`

`=(0.05)/(√(65))`

= 0.00620174

By applying the Z-score formula:

x = μ + ( Z × σ )

`\bar x = \mu _(\bar x) +(Z * \sigma _(\bar x))`

`\bar x = 0.45 + (-1.65 *0.00620174)`

`\bar x= 0.439767129`

`\bar x \approx 0.44 \ inches`