Question

Your local school board wants to determine the proportion of people who plan on voting for the school levy in the upcoming election. They conduct a random phone poll, where they contact 150 individuals and ask them whether or not they plan on voting for the levy. Of these 150 respondents, 78 people say they plan on voting for the levy. The school board wants to determine whether or not the data supports the idea that more than 50% of people plan on voting for the levy. Conduct a hypothesis test at the 0.10 significance level to test this claim.

Answer 1

There is not enough evidence to conclude that the data supports the idea that more than 50% of people plan on voting for the levy

Explanation:

Sample size, n = 150

Number of people that plan on voting for the levy, X = 78

Proportion of people that plan on voting for the levy:

`\bar{p} = X/n\\\bar{p} = 78/150\\\bar{p} = 0.52`

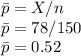
The study is to determine whether or not the data supports the idea that more than 50%(0.5) of people plan on voting for the levy

The null and alternative hypotheses are:

`H_0: p \leq 0.5\\H_a: p > 0.5`

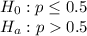
Calculate the test statistics:

`t_s = \frac{\bar{p} - p}{\sqrt{(p(1-p))/(n) } } \\t_s = \frac{0.52-0.5}{\sqrt{(0.5(1-0.5))/(150) } } \\t_s = 0.49`

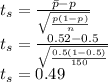
For a test statistic
`t_s = 0.49`, the p-value = 0.3121

The significance value,
`\alpha = 0.10`

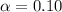
Since the p-value(0.3121) is greater than α(0.10), the null hypothesis
`H_0` will be accepted.

This means that there is not enough evidence to conclude that the data supports the idea that more than 50% of people plan on voting for the levy