Question

Two large containers A and B of the same size are lled with different uids. The uids in containers A and B are maintained at 0° C and 100° C, respectively. A small metal bar, whose initial temperature is 100° C, is lowered into container A. After 1 minute the temperature of the bar is 90° C. After 2 minutes the bar is removed and instantly transferred to the other container. After 1 minute in container B the temperature of the bar rises 10°. How long, measured from the start of the entire process, will it take the bar to reach 99.9° C?

Answer 1

Answer: t = 9.05 min

Explanation: The rate of temperature over time is given by:

`(dT)/(dt) = k (T - T_c)`

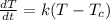
where:

K is the constant of transference of heat

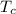`T_c` is temperature of the container

`\int\limits^a_b {(1)/(T-T_c) } \, dT = \int\limits^a_b {k} \, dt`

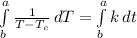
ln (T -
`T_c`) = kt + c

`e^(kt+c) = T - T_c`

`Ce^(kt) = T - T_c`

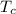`T = Ce^(kt) + T_c`

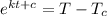
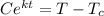
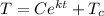
In container A, the temperature is at 0°C, so

`T = Ce^(kt) + 0`

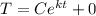
For the bar, when t = 0 min, T = 100°C:

`T = Ce^(kt)`

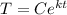
100 =
`Ce^(k.0)`

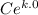
C = 100

After 1 minute, the temperature of the bar is 90°C, so:

`T = 100e^(kt)`

`100e^(k.1) = 90`

`e^(k) = (90)/(100)`

`ln (e^k) = ln (0.9)`

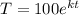
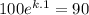
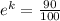
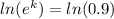
k = ln(0.9)

k = - 0.105

`T = 100e^(-0.105t)`

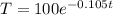
After 2 minutes, the temperature will be:

`T = 100e^(-0.105.2)`

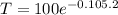
T = 81.06°C

For container B, the temperature is 100°C, so:

`T = Ce^(kt) + T_c`

`T = Ce^(kt) + 100`

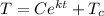
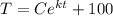
The initial temperature of the bar when entering the container B is T = 81.06°C, then:

`81.06 = Ce^(k.0) + 100`

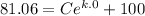
C = - 18.94

After 1 minute, the temperature rises 10°C:

`T = - 18.94e^(kt) + 100`

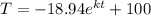
91 =
`- 18.94e^(k.1) + 100`

`e^(k) = (9)/(18.94)`

`e^(k) = 0.475`

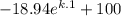
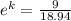
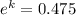
k = ln(0.475)

k = - 0.744

`T = - 18.94e^(-0.744t) + 100`

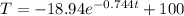
When T = 99.9°C:

`99.9 = - 18.94e^(-0.744t) + 100`

`e^(- 0.744t) = (99.9 - 100)/(- 18.94)`

`e^(-0.744t) = 0.0053`

t =
`(ln(0.0053))/(-0.744)`

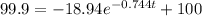
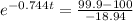
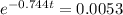
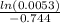
t = 7.05 min

The entire process will take:

t = 2 + 7.05

t = 9.05 min