Question

Concept Simulation 20.4 provides background for this problem and gives you the opportunity to verify your answer graphically. How many time constants (a decimal number) must elapse before a capacitor in a series RC circuit is charged to 39.0% of its equilibrium charge

Answer 1

Answer: t = 0.492τ

Explanation: In a circuit where there is a resistor and a capacitor, the equation for a charging capacitor is given by:

`q = q_0(1 - e^{(t)/(RC) })`

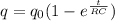
where:

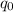`q_0` is the equilibrium charge

q is the charge at time t

RC is time constant also called τ (tau)

For this problem, the circuit is charged to 39%, which means: q =
`0.39 q_0`

`0.39q_0 = q_0 (1 - e^(-t)/(RC) )`

0.39 = 1 -
`e^(-t)/(RC)`

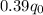
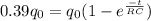
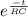
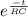`e^(-t)/(RC)` = 0.61

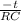`(-t)/(RC)` = ln(0.61)

-t = ln(0.61)τ

t = 0.492τ

For the condition to be met it is needed 0.492 time constants must elapse.