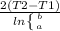Question

(a) A spherical shell has inner and outer radii a and b, respectively, and the temperatures at the inner and outer surfaces are T2 and T1, respectively. The thermal conductivity of the material of which the shell is made is k. Derive an equation for the total heat current through the shell. (b) Derive an equation for the temperature variation within the shell in part (a); that is, calculate T as a function of r, the distance from the center of the shell. (c) A hollow cylinder has length L, inner radius a, and outer radius b, and the temperatures at the inner and outer surfaces are T2 and T1, respectively. (The cylinder could represent an insulated hot-water pipe, for example.) The thermal conductivity of the material of which the cylinder is made is k. Derive an equation for the total heat current through the walls of the cylinder.

Answer 1

A) H = 4K(T2-T1) / b -a

B) T(r) = T2 - ( T2 - T1 )*((r-a)/(b-a)) *(b/r)

C) H = 2(T2-T1) / ln
`\left \{ {{b} \atop {a}} \right}.`

Step-by-step explanation:

Inner radii = a

outer radii = b

thermal conductivity = k

difference between inside and outside shell = dt

surface area of sphere = 4
`\pi r^2`

surface area of the curved side of a cylinder = 2
`\pi rl`

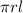
A) An equation for the total heat current through the shell

using the formula for thermal conductivity of a material which is H =
`(kAdt)/(dr)`

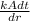
H =
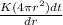`(K(4\pi r^2)dt)/(dr)` therefore
`(Hdr)/(4\pir^2 ) = kdt` ---------- equation 1

integrate equation 1 using a and b as limits

`(H)/(4\pir^2 ) ((1)/(a) - (1)/(b)) = k (T2-T1)`

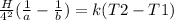
if T2 > T1 then change in temperature
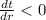`(dt)/(dr) < 0` hence H =
`(4K\piab(T2-T1) )/(b-a)`

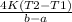
B) Derive an equation for the temperature variation within the shell in part A

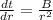`(dt)/(dr) = (B)/(r^2)` --------- equation 2

B =
`(H)/(4\pi k)`

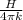
integrating equation 2 from r = a to r

T(r) - T2 = B
`((1)/(a)-(1)/(r))`

also integrating equation 2 from r = a to r = b

T1 - R2 = B
`((1)/(a)-(1)/(b))`

eliminate B by using the second integration gives the equation as

T(r) = T2 - ( T2 - T1 )
`((r-a)/(b-a) )((b)/(r) )`

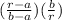
if r = a T = T1 and at r = b; T = T1

C) An equation for the total heat current through the walls of the cylinder

H = k ( 2
`\pi rl` )
`(dt)/(dr)`

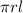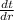
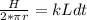`(H)/(2*\pi r ) = kLdt` ----- equation 3

integrating equation 3 within given limits a and b

`(H)/(2*\pi r) ln ((b)/(a) ) = kL ( T2 - T1 )`

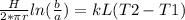
therefore H =
`\frac{2\pikL(T2 - T1) }{ln\left \{ {{b} \atop {a}} \right. }`