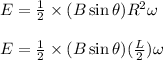Question

A baton twirler is twirling her aluminum baton in a horizontal circle at a rate of 2.33 revolutions per second. A baton held horizontally. Calculate the induced emf between the center and one end of the baton if the magnetic field of the Earth is 0.500 gauss and is oriented at 14.42 with respect to the horizontal. Assume the baton is 60.1 cm in length.

Answer 1

Step-by-step explanation:

Given that;

horizontal circle at a rate of 2.33 revolutions per second

the magnetic field of the Earth is 0.500 gauss

the baton is 60.1 cm in length.

the magnetic field is oriented at 14.42°

we wil get the area due to rotation of radius of baton is

`\Delta A = (1)/(2) \Delta \theta R^2`

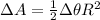
The formula for the induced emf is

`E = (\Delta \phi)/(\Delta t)`

`\phi = \texttt {magnetic flux}`

`E=(\Delta (BA) )/(\Delta t)`

`=B(\Delta A)/(\Delta t)`

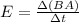
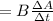
B is the magnetic field strength

substitute

`\texttt {substitute}\ (1)/(2) \Delta \theta R^2 \ \ for \Delta A`

`E=B((\Delta \theta R^3/2))/(\Delta t) \\\\=(1)/(2) BR^2\omega`

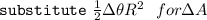
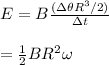
The magnetic field of the earth is oriented at 14.42

`\omega =2.33\\\\L=60.1c,\\\\\theta=14.42\\\\B=0.5`

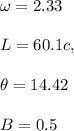
we plug in the values in the equation above

so, the induce EMF will be

`E=(1)/(2) * (B\sin \theta)R^2\omega\\\\E=(1)/(2) * (B\sin \theta)((L)/(2) )\omega`

`=(1)/(2) *0.5gauss*(0.0001T)/(1gauss) *\sin 14.42*((60.1*10^-^2m)/(2) )^2(2.33rev/s)((2\pi rad)/(1rev) )\\\\=2.5*10^-^5*0.2490*0.0903*14.63982\\\\=2.5*10^-^5*0.32917\\\\=8.229*10^-^6V`