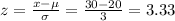Question

1. (6.2 lesson) Calculate the value of z. (Round to the hundredth) *

z

18

520

22.84

O 29.24

O O O O

18.24

0.04

This is a required question

Answer 1

The answer is explained below

Explanation:

The question is not complete, I would explain how to calculate the value of Z

The z score is a measure in statistic used to determine the number of standard deviations by which the raw score if from the mean of a normal distribution. If the z score is positive then the raw score is above the mean while if a z score is negative the raw score is below the mean. The z score (z) is given by the formula:

`z=(x-\mu)/(\sigma)`

Where x is the raw score, μ is the mean and σ is the standard deviation.

Let us assume that the mean (μ) = 20 and the standard deviation (σ) = 3. To calculate the z score for x = 30 it is given by:

`z=(x-\mu)/(\sigma)=(30-20)/(3)=3.33`