Question

EXTREAMLY URGENT!!!PLEASE COME AND JUST TAKE A LOOK!!! WhAT is the distance formula for the distance between points K and L?

Answer 1

`d = \sqrt{(0+3)^(2) + (3-3)^(2) + (-3+3)^(2)}`

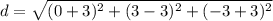
Explanation:

The distance formula for (x, y, z) is the same as the distance formula for (x, y), but with just one more added variable:
`d = \sqrt{(x2-x1)^(2) + *y2-y1)^(2) + (z2-z1)^(2)}`

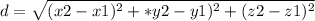
If that is the case, we just plug in x, y, and z. But wait, we are missing point K coordinates. Simple enough. Point K is just a translation of point L by moving to the left. That means the coordinates are the same except for x, which will be -3 (so the coordinates would be (-3, 3, -3)). That just leaves us to plug it into the equation:

`d = \sqrt{(0--3)^(2) + (3 - 3)^2 + (-3--3)^2}`

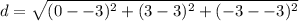
Simplifying it down gives you the answer in the answer. If you want to find an exact value, simply plug it into the calc. That will give you d = 3.