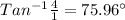Question

A Honda Civic and an 18 wheeler approach a right angle intersection and then collide. After the collision, they become interlocked. If their mass ratios were 1: 4 and their respective speeds as they approached were both 13 m/s, find the magnitude and direction of the final velocity of the wreck. (Please do not worry no one was harmed in making of this question) A. 16.3 m/s at 79° B. 10.7 m/s at 79° C. 12.5 m/s at 59° D. 15.7 m/s at 59°

Answer 1

The concept of conservation of momentum is applied in the particular case of collisions.

The general equation ig given by,

`M_1V_1 + M_2V_2 = (M_1+M_2) * V_f,`

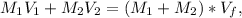
Where,

`M_2 = 4 M_1`

The crash occurs at an intersection so we must separate the two speeds by their respective vector: x, y.

In the case of the X axis, we have that the body
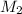`M_2` has a speed = 0, this because it is not the direction in which it travels, therefore

`M_1* 13 = (M_1+M_2) * V_(fx) \\M_1*13 = (M_1+4M_1)*V_(fx)\\M_1*13=5M_1*V_(fx)\\Vx = (13)/(5)m/s`

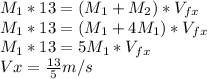
The same analysis must be given for the particular case in the Y direction, where the mass body
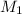`M_1` does not act with its velocity here, therefore:

`M_2* 13 = (M_1+M_2) * V_(fy),\\4*M_1* 13 = 5Ma * V_(fy) ,\\V_(fy) = (52)/(5)m/s ,`

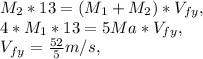
We have the two components of a velocity vector given by
`V_f = (13)/(5)\hat{i} + (52)/(5)\hat{j}`

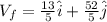
Get the magnitude,

`V_f = \sqrt{((13)/(5))^2+((52)/(5))^2}`

`V_f = 10.72 m/s`

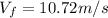
With a direction given by

`Tan^(-1) (4)/(1) = 75.96 \°`